Records 2

2021-11-14

以下记录了 NOIP 2021 前做题中的思路/关键点。
题号后 (x/y) 代表个人认为该题的思维难度/代码难度。

1. CF402E Strictly Positive Matrix (4/1)

   • 题目中询问是否含有 $0$，所以可以将所有 $a_{i,j} \neq 0$ 设为 $1$。
   • 转化后是邻接矩阵的形式，$a_{i,j} = 1$ 代表 $i$ 向 $j$ 连边。设邻接矩阵为 $G$，则 $G^k_{i,j}$ 代表 $i$ 到 $j$ 之间是否有长度为 $k$ 的路径。
   • 题目中保证至少存在一个自环，则说明我们可以选取一个很大的 $k$，利用自环满足上述关于 $G^k_{i,j}$ 的要求。
   • 至此，题目转化为了邻接矩阵 $G$ 代表的图中所有点是否属于一个强连通分量，tarjan 缩点即可。

2. CF427C Checkposts (1/2)

   • 缩点后统计每个强连通分量中最小值及其出现次数即可。

3. CF981D Bookshelves (3/1)

   • 贪心地考虑，高位选 $1$ 肯定比低位都选 $1$ 要更优，所以从高位向低位进行 dp。
   • 我们希望验证当前枚举到的 $x$ 是否能够作为答案，设 $f_{i,j}$ 为前 $i$ 本书放在 $j$ 个书架上能否组成 $x$，转移为 $f_{i,j} |=f_{k,j-1} \& [(\sum\limits_{p=k+1}^{i}\& x)=x]$。

4. P4377 [USACO18OPEN] Talent Show G (3/2)

   • 如果题目没有最小重量为 $W$ 的限制，那么直接贪心，通过 01 分数规划按照 $a_i-b_ix$ 排序。
     • 考虑对于限制进行 01 背包，把所有总质量 $\ge W$ 的更新全算在 $f_W$ 上。

5. P3031 [USACO11NOV] Above the Median G (2/1)

   • 套路题，将 $\ge x$ 的数设为 $1$，$<x$ 的数设为 $-1$，计算前缀和逆序对数即可。

6. P3008 [USACO11JAN] Roads and Planes G (2/2)

   • spfa 会被卡，考虑用 dijkstra。注意到双向边没有负边权，缩点后单向边是 DAG。强连通分量内部用 Dijkstra，强连通分量之间拓扑排序即可。
   • 注意有负边权，询问是否连通时需要询问一个略小于初始设定的 INF 的数。

7. P7677 [COCI2013-2014#5] LADICE (2/1)

   • （可以二分图匹配，但没有必要）。
   • 并查集维护对于每个联通块，如果边数大于点数则新加入的边不合法，否则合法。

8. P4443 [COCI2017-2018#3] Dojave (4/2)

   • 正难则反，考虑有多少个序列不合法。
   • 通过一系列讨论发现：一段连续子序列不合法的充要条件是这段连续子序列的长度是 $4$ 的倍数并且连续子序列里面的数两两配对的异或值为 $2^n-1$。
   • 一段长为 $4$ 倍数的区间异或和为 $0$ 是这个区间两两配对的必要条件。我们将配对的一组数赋成同一个较大的随机数（Hash 的思想），如果区间异或和仍为 $0$ 则可以认为该区间满足条件。
   • 单哈希会被卡，用双哈希。

9. CF340D Bubble Sort Graph (2/1)

   • 题目可以理解为给出一个长度为 $n$ 的序列，每个逆序对连一条无向边，求得到的无向图（可能不连通）的最大独立集。
   • 不难发现没有连边的点肯定不是逆序的（因此是递增的），所以将原题转化为了 $\Theta(n \log n)$ LIS 裸题。

10. CF617E XOR and Favorite Number (2/3)

    • 处理前缀异或和，将问题转化为求 $[l,r]$ 中有多少对 $(i,j)$ 满足 $a_i \text{xor} a_j=k$。
    • 静态区间离线查询，考虑使用莫队算法解决。

11. CF161D Distance in Tree (3/1)

    • （点分治模板题，可惜我不会）
    • 一题多解，树形 dp，树上启发式合并，长链剖分，点分治均可以做。
    • 发现 $k$ 很小，考虑使用 $\Theta(nk)$ 的树形 dp 解决。设 $f_{i,j}$ 为以 $i$ 为根的子树中距离根距离为 $j$ 的点有多少个，回溯时向上暴力统计答案即可。

12. CF980E The Number Games (2/2)

    • 贪心，选 $n$ 号城市一定比选 $[1,n-1]$ 的所有城市要优。将 $n$ 号节点定为树根，按编号从大到小枚举节点，如果该节点到根的路径上没有选的点数小于等于剩下还能选的点数，则将整条路径选中。
    • 树剖 + 线段树实现，线段树支持区间赋值为 $1$，区间求和。

13. CF1101F Trucks and Cities (4/2)

    • 发现题目可以抽象成序列上的区间问题，考虑区间 dp。设 $f_{i,j,k}$ 为从 $i$ 到 $j$ 划分成 $k$ 段后最长段的最小值。暴力转移可以考虑枚举最右段的左端点 $l$，则有 $f_{i,j,k}=\min\limits_{l=i}^{j}\{\max\{f_{i,l,k-1},a_j-a_l\}\}$，复杂度 $\Theta(n^4+m)$。
    • 可以发现 $f_{i,l,k-1}$ 单调递增，$a_j-a_l$ 单调递减，用指针单调地更新 $l$ 的值，每次转移就变成了在 $l-1$ 和 $l$ 中决策，复杂度降至 $\Theta(n^3+m)$。

14. CF1408E Avoid Rainbow Cycles (3/1)

    • 重构一张图，将集合看作一个点，向所有集合内的元素连边，不难发现如果新图中有环则在原图上不合法。在新图上求最大生成树，删除其余的边即可。

15. CF274E Mirror Room (4/3)

    • 见题解。

16. P2737 [USACO4.1] 麦香牛块 Beef McNuggets (3/1)

    • 关于上界的证明见 __rqy 的证明： https://www.luogu.com.cn/blog/rqy/solution-p2737
    • 确定枚举的上界后，背包考虑每个元素是否能被凑出。具体地，如果 $k$ 能被凑出，则 $k+a_i$ 也能被凑出。

17. P4269 [USACO18FEB] Snow Boots G (3/2)

    • 考虑将地板和靴子放在一起排序，如果是地板就线段树上单点修改为 $0$，是靴子就查找全局最长的连续的 $1$ 的个数即可，具体做法为 P2572 [SCOI2010] 序列操作 的弱化版。

18. CF1101G (Zero XOR Subset)-less (4/1)

    • 首先需要先知道什么是线性基及其性质。（见 OI-Wiki）
    • 首先套路地用前缀和将 $[l,r]$ 的异或和转化为 $pre_{l-1} \text{xor} pre_r$。 有下面的结论：把 $pre_i$ 依次插入线性基，如果能成功插入答案加 $1$。
    • 设 $b_1,b_2,\cdots,b_m$ 为成功插入线性基的下标，对于任意 $(b_i,b_j)$ 的异或值均不为 $0$，而这恰好是 $pre$ 中某一段的异或和，因此任意段异或和不为 $0$。

19. P3041 [USACO12JAN] Video Game G (2/2)

    • AC 自动机上 dp，套路地有 $f_{i,j}$ 为当前考虑到第 $i$ 位，在 trie 树上走到 $j$ 号节点时的最大得分。记每个单词结尾点 $i$ 有分值为 $ed_i$，则对于每个节点更新 fail 时要直接加上其 fail 的分值。转移方程 $f_{i,tr_{j,son}}=\max\{f_{i-1,j}+ed_{tr_{j,son}}\}$。

20. CF343C Read Time (2/2)

    • 显然时间越长，每个点能移动的距离越大，覆盖的范围也越远。因此答案具有单调性，考虑二分答案。
    • 贪心地考虑覆盖一段，并维护当前点的左右指针。当右指针指向 $m+1$ 说明整个区间均被覆盖，当前答案合法。

21. P3119 [USACO15JAN] Grass Cownoisseur G (3/3)

    • 考虑缩点时统计强连通分量的大小，记为新点的点权。
    • 缩点后对新图正反方向连边，跑最长路后枚举需要反向的边，统计答案。

22. P7914 [CSP-S 2021] 括号序列 (5/3)

    • 为防止循环变量混淆，将题目中关于连续 * 的限制设为 $m$。定义 A、B 为合法的超级括号串，S 为题目中所述的连续不超过 $m$ 个的 *。
    • 区间 dp，考虑设 $f_{i,j}$ 为 $[i,j]$ 中形如 (A)、(AS)、(SA) 的超级括号串个数，即满足 $i,j$ 位置上的括号匹配的合法超级串个数；设 $g_{i,j,0}$ 为 $i,j$ 区间内形如 AB、ASB 的超级括号串个数，即 $i,j$ 位置上分别是左右括号，但不匹配；设 $g_{i,j,1}$ 为 $[i,j]$ 区间内形如 AS 的串的个数，即一个合法超级括号串右边加 $(0,\min\{m,j-i-1\}]$ 个 * 能组成的串的个数（相当于一个后缀和，将 $\Theta(n^4)$ 的 dp 优化成 $\Theta(n^3)$）。
    • 转移方程：
      • $f_{i,j}=g_{i+1,j-1,0}+g_{i+1,j-1,1}+\sum\limits_{k=1}^{\min\{m,j-i-1\}}g_{i+k+1,j-1,0}$
      • $g_{i,j,0}=f_{i,j}+\sum\limits_{k=i+1}^{j-2}(g_{i,k,0}+g_{i,k,1})\times f_{k+1,j}$
      • $g_{i,j,1}=\sum\limits_{k=1}^{\min\{m,j-i\}}g_{i,j-k,0}$
    • 转移顺序：$g_{i,j,1}\rightarrow f_{i,j}\rightarrow g_{i,j,0}$，转移 $f_{i,j}$ 前需要判断 $[i,j]$ 是否合法（即 $i,j$ 位置上分别为左括号和右括号，可以用 ? 代替），转移连续的 * 时遇到括号则 break。

23. CF242E XOR on Segment (2/2)

    • 发现异或和区间加不方便同时在线段树上维护，所以考虑拆位，异或操作则为按位取反，区间求和时将第 $i$ 位 $1$ 的个数乘以 $2^i$ 即可。

24. CF803G Periodic RMQ Problem (3/4)

    • 动态开点保证了空间，询问最小值的时候用 ST 表维护。若区间被覆盖过则为覆盖的值，否则分三类讨论：$[l,r]$ 包含了至少一个区间长度，不到一个区间长度且被一个完整区间包含，不到一个区间长度且跨过两个区间。
    • 下标整体左移方便处理边界。

25. P3605 [USACO17JAN] Promotion Counting P (2/1)

    • 树状数组 + dfs，离散化后在树上对于每个点询问前 $ans_x$ 先减去已经比 $x$ 大的数的个数，搜完 $x$ 的子树后再加上新的差值，即 $x$ 子树中比 $x$ 大的数的个数。

26. P2943 [USACO09MAR] Cleaning Up G (3/1)

    • 令人耳目一新的思维好题。
    • 发现从当前位置往前跳，最多跳 $\sqrt{n}$ 个不同的数字，否则肯定不优。利用这个性质可以将 dp 优化到 $\Theta(n\sqrt{n})$。

27. P4375 [USACO18OPEN] Out of Sorts G (3/1)

    • 将序列离散化，发现每次双向冒泡排序的时候，若一个位置 $x$ 前的数没有排好序，则每次双向冒泡排序是将一个大于位置 $x$ 的数换出去，再将一个小于位置 $x$ 的数换回来，即答案为 $\max\{$位置$ x$ 之前有多少个数大于 $x\}$。

28. CF620E New Year Tree (2/3)

    • 将树上问题通过 dfn 序映射到序列上，线段树维护。注意到颜色种类很少，状压后可以存在 long long 范围中。

29. P1941 [NOIP2014 提高组] 飞扬的小鸟 (2/3)

    • 又是一道咕了不知道多久的经典题。
    • 背包的 dp 思路很显然，上升时完全背包，下降时 01 背包。题目中有非常多需要仔细处理的细节，比如管道真正的边界在哪里，上界超过 $m$ 的转移到 $m$（开大数组！），不能通过是输出答案的边界判断等等。

30. CF343D Water Tree (1/2)

    • 又水了一道树剖的板子。

31. CF1100E Andrew and Taxi (3/3)

    • 考虑二分答案，每次只对于删不掉的边考虑是否有环。如果没有环则答案合法。找到答案后，将所有拓扑序逆序的边反向即可。

32. CF1131F Asya And Kittens (2/1)

    • 注意到合并两个块的时候，块内顺序是不可以改变的，所以 vector 暴力合并即可。（把小的 vector 暴力 push 到大的上）

33. CF711D Directed Roads (1/2)

    • 不难发现题目中给定了一个基环森林，对于每个环上的边只要不朝向同一方向即可。所有不在环上的边方向任取。

34. CF85E Guard Towers (3/2)

    • 最大值最小，可以想到二分答案；分成两部分，可以想到二分图。二分距离最大的两点的距离最小值，将大于 mid 的点之间连边，dfs 染色（不用真存边，dfs 染色遍历即可）。如果能够黑白染色，说明取当前 mid 合法。
    • 设联通块的个数为 $cnt$，则总方案数为 $2^{cnt}$，因为二分图中任意一个联通块的左部点和右部点均可互换。

35. CF632F Magic Matrix (3/1，指暴力)

    • 正解是神仙建图跑最小生成树，复杂度 $\Theta(n^2\log n^2)$。
    • 但发现 $n\leq 2500$ 且时限 5s，$\Theta(\frac{n^3}{\omega})$ 可以卡过。暴力的思想就是对于每个点的数值从小到大排序加入矩阵，每次加入时查找第 $i$ 行和第 $j$ 行的第 $k$ 位是否都小于 $a_{i,j}$，如果是则不合法。用 bitset 维护上述操作，因为从小到大加入数字，所以已经加入的在 bitset 中赋为 $1$，查找时只需要查找 $i,j$ 位置上是否至少有一个 $0$ 即可。

36. CF476D Dreamoon and Sets (3/1)

    • 贴一个题解的分析：

    

37. CF40E Number Table (4/1)

    • 思维好题。发现 $k<\max\{n,m\}$ 这个条件很特殊，它保证了无论如何填数都有一个空行和一个空列。
    • 不妨设 $n>m$。所有列都可以通过空行满足要求，对于每行也利用空出的列满足要求。如果有某一行或某一列已经填满且乘积为 $1$ 则必然无解，行列个数的奇偶性不同也会导致空行空列的交点处无法满足条件，因此也无解。如果有解，且某一行没有填满，则除了需要留下一个格子空着不填，剩余的格子随意。因此答案为 $\prod\limits_{i=1}^{n} 2^{m-cnt_i-1}$。

38. CF17E Palisection (4/2)

    • 正难则反，考虑用总的方案数减去不相交的方案数。设 $f_i$ 为以 $i$ 为右端点的回文串个数，$g_i$ 为以 $i$ 为左端点的回文串个数，则答案为 $\sum\limits_{i=1}^{n}f_i\sum\limits_{j=1}^{i-1}g_i$。
    • 用 manacher 求出所有位置的回文半径，发现本质上就是区间加 $1$，前缀和 + 差分即可。复杂度 $\Theta(n)$。

39. CF949C Data Center Maintenance (3/2)

    • 阅读理解题。读懂题意后发现题目让求必须选一个点推迟的情况下需要推迟的最小点数。tarjan 缩点后贪心地考虑所有 DAG 上出度为 $0$ 的点，取最小的即为答案。

40. P2938 [USACO09FEB] Stock Market G (2/1)

    • 怎么普及组难度的 dp 都要调好久啊……
    • 本题的转化在于股票的买卖，因为一天内可以无限次买入卖出，所以 $x$ 天前购买的股票可以看作在第 $x+1$ 天又买入后卖出，以此类推。完全背包即可。

41. CF1110C Meaningless Operations (2/1)

42. P4878 [USACO05DEC] Layout G (1/2)

43. CF540C Ice Cave (1/1)

44. 1103 模拟赛 - planning (4/1)

    • 题意是说有 $n$ 栋楼房高度为 $h_i$，现在操作 $k$ 次，每次可以改变任意一栋楼房的高度，使相邻两楼房之间的高度差最大值最小。形式化地，可以进行 $k$ 次操作使 $h_i=b$，最小化 $\max\limits_{i=2}^{n}\{h_i-h_{i-1}\}$。$1\le k\le n\le 2000$。
    • 二分答案 + dp。dp 时设 $f_i$ 为对于前 $i$ 栋楼房，在不修改第 $i$ 栋的前提下满足当前二分值的最小修改次数。转移时如果对于 $1 \leq j < i$， $|h_i-h_j|$ 不超过二分值的 $i-j$ 倍则可以在 $f_j$ 基础上修改 $i-j-1$ 栋楼房达到目的。统计答案时如果满足 $\exists i\in[1,n],f_i+(n-i) \leq x$ 即合法。

45. 1103 模拟赛 - garland (5/2)

    • 题意是要求求出环形最大 $m$ 段和。$1\le m\le 10^5,1\le n\le 3\times 10^5$。
    • 首先对于每一段连续的值为正或值为负的数字，如果选则选完一整段。将原序列缩成一个正负相间的环，考虑 $m$ 次是否能选完所有正的区间，如果不能则需要做出牺牲。
    • 我们需要放弃一些值为正的区间或选上一些值为负的区间来连接两个正区间。一个思路是按照区间价值的绝对值贪心，但这个贪心策略有一定的问题：如果想要选择两个负区间来连接三个正区间，但此时中间的正区间却已经被删除，那我们就失去了这种选择。所以考虑反悔贪心，选择一个区间时，可以将其左右区间删除并将连续的三个区间之和插入原位置，如果这个位置再次被选到则说明贪心需要反悔。用堆和双向链表维护，时间复杂度 $\Theta(n\log n)$。

46. 1103 模拟赛 - cipher (3/3)

    • 题意是给定一个长度为 $n$ 操作序列形如 XOR a，AND b，OR c，再有 $m$ 次操作每次询问一个数经过整个操作序列后的结果，或者修改操作序列的某一个数。$n,m\le 2\times 10^5$。
    • 显然要按位处理，用线段树维护。对于每个节点 $t_{0/1,i,p}$ 表示第 $i$ 位经过左端点前的 $0/1$ 经过 $p$ 节点所代表的区间得到的结果，这样就有了结合律，可以区间维护。

47. CF1348B Phoenix and Beauty (2/1)

    • 发现最终序列长度的限制很宽松，达到了 $n^2$ 级别，所以直接考虑构造一个长度为 $k$ 且包含原序列中所有元素的序列 $b$，将其复制 $n$ 遍得解。注意如果原序列中数字的种类大于 $k$ 则无解。

48. CF1312E Array Shrinking (2/2)

    • 经典 dp 题，考虑首先区间 dp 计算出每个区间能缩成的值，如果一个区间不能缩成一个数则为 $0$，复杂度 $\Theta(n^3)$。再考虑统计答案，枚举当前位置和其之前的一个位置，如果组成的区间可以合并成一个数则转移，复杂度 $\Theta(n^2)$。

49. CF1110E Magic Stones (3/1)

    • 如果边界不相等一定无解。
    • 设 $d$ 为差分序列，即 $d_i=c_i-c_{i-1}$。每次操作我们改变 $c_i$ 的同时，$d_i$ 会发生如下改变：$d_i=(c_{i+1}+c{i-1}-c_i)-c_{i-1}=c_{i+1}-c_i, d_{i+1}=c_{i+1}-(c_{i+1}+c{i-1}-c_i)=c_i-c_{i-1}$，本质上就是差分数组的相邻元素互换。将 $c,t$ 差分，判断两个差分数组排序后是否相等即可。

50. CF989C A Mist of Florescence (3/1)

    • 好题。将 $50\times 50$ 的棋盘横向分成四部分，一部分一个字符充当背景。增加一个字符的连通块个数只需要在另外一个字符的背景下更改单个独立的字符即可。

51. P4372 [USACO18OPEN] Out of Sorts P (4/2)

    • 求每次冒泡排序操作的序列长度，就是求每个点被冒泡排序的次数。
    • 如果序列所有点两端都有分割线，则序列是排好序的。将原序列离散化，一条分割线出现的时间就是离它最远的小于它的点冒泡到它前面的时间，可以用指针维护。

52. P3045 [USACO12FEB] Cow Coupons G (4/2)

    • 贪心反悔。首先一个显然错误的贪心思路是按折扣价从小到大贪心地选，但我们发现可能会出现让折扣价相对不优的获得折扣，并让一个先前被认定要折扣的物品恢复原价可能更优的情况。
    • 先将前 $k$ 小的 $c_i$ 值放入小根堆，考虑用剩余的钱贪心地购买物品。对于后 $n-k$ 个物品中的第 $j$ 个，它的花费可能是 $p_j$（不用优惠劵）或 $p_j+c_i-c_j$。所以用三个优先队列分别维护 $c_i$，$p_i$ 和 $p_i-c_i$ 即可。

53. CF1348D Phoenix and Science (1/2)

    • 贪心地想可能每次让变化量增长最多是最优的。但我们需要结果恰好为 $n$，直接找到第一个比依次减去若干个二的整次幂后的剩余量小的位置插入，再差分即可。

54. CF1304D Shortest and Longest LIS (2/1)

    • 对于最长 LIS，构造序列 $a_i=i$，再翻转所有连续为 > 的区间。反之同理。

55. CF1286C1 Madhouse (Easy version) (3/2)

    • （Hard version 暂时咕了）
    • 可以询问 $[1,n]$ 和 $[1,n-1]$，总询问的字串长度是 $n^2$ 满足 Easy version 题目的限制。询问 $[1,n]$ 会比 $[1,n-1]$ 多出 $n$ 个子串，找到这些乱序的子串（后缀）就可以恢复原串。
    • 找子串时用 multiset，将 $[1,n]$ 的每个子串按字母顺序排序后插入可重集，再对于 $[1,n-1]$ 的每个子串执行删除操作，最后 multiset 中便剩余了所需要的 $n$ 个后缀。

56. CF335F Buy One, Get One Free (5/2)

    • orz xixike
    • 我们将价值相同的物品放在一起，记录对于每个价值共有多少个。对于每一组物品，可以通过选择更换堆顶，或保留堆顶并向堆中插入 $2\times val-k$ 的代价，代表全价购买了 $k$，但免费可以选择两个价值为当前值 $val$ 的物品。注意对于每一组物品，考虑时应将这一轮需要插入堆中的物品用数组记下，等操作完这一轮再加入堆中，以防冲突。

57. P5017 [NOIP2018 普及组] 摆渡车 (3/1)

    • 显然我是来填坑的。
    • 不需要斜率优化的做法好想好写，就没写斜率优化。考虑将时间轴分段，将每次摆渡车出发的时间视为右端点，问题便转化为将时间轴分为若干长度 $\ge m$ 的段，使每个点到其所在段的右端点距离和最小。
    • 设 $f_i$ 代表时间为 $i$ 的最优决策，注意考虑边界，带 $\sum$ 的式子不方便直接维护所以用前缀和优化；每次只需要从 $(i-2m,i-m]$ 转移，并且在 $(i-m,i]$ 若没有点则 $f_i$ 可以直接继承 $f_{i-m}$ 的答案。时间复杂度 $\Theta(nm^2+t)$。

58. 1105 模拟赛 - treasure (4/3)

59. 1105 模拟赛 - path (3/2)

    • 出题人脚造数据，直接让最短路水过差评。
    • 正解是 bfs，首先将和起点连接的所有边权为 $0$ 的边缩成一个点进行 bfs，因为前导零没有贡献。然后按照顺序分组更新，对于每一层扩展按照 $0,1$ 的顺序分组更新即可。

60. P2986 [USACO10MAR] Great Cow Gathering G (2/2)

    • 换根 dp 模板。先算出对于每个点，这个点的子树都聚集到它的花费，发现根节点 $1$ 的花费就是一个可行解。考虑每次换成一个子节点，改变的贡献可以 $\Theta(1)$ 求出。总复杂度 $\Theta(n)$。

61. P3066 [USACO12DEC] Running Away From the Barn G (2/2)

    • 发现距离小于等于 $t$ 这个限制等价于将树上连续的一段进行区间加，可以使用树上差分。暴力向上跳 $t$ 的长度复杂度为 $\Theta(nt)$，可以倍增优化成 $\Theta(n\log t)$。

62. P3047 [USACO12FEB] Nearby Cows G (3/2)

    • 树形 dp 经典题，记 $g_{i,j}$ 为 $i$ 的子树中距离 $j$ 以内的点的点权和，$f_{i,j}$ 为距离点 $i$ 在 $j$ 以内的点的点权和。$g_{i,j}$ 直接求，$f_{i,j}$ 考虑容斥，有 $f_{i,j}=g_{i,j}+f_{fa_{i},j-1}-f_{i,j-2}$。

63. P3660 [USACO17FEB] Why Did the Cow Cross the Road III G (3/1)

    • 考虑按照两个字符出现的间距从大到小排序，然后依次插入树状数组中。因为从大到小排序，后加入树状数组的区间不可能同时包含先加入树状数组的区间的左右端点。按顺序修改左右端点，区间求和即可。

64. P3071 [USACO13JAN] Seating G (2/3)

    • 不难想到用线段树维护。对于每个区间存储左/右/整体最长连续空区间的长度，用于区间的修改和合并。查询第一个空着的长度为 $k$ 的段，只需要通过线段树根节点判断是否合法，再直接二分查询即可。注意如果是左右子树合并起来的区间满足条件，直接返回一个确定的左边界即可。

65. 1106 模拟赛 - chess (3/1)

    • 题意不够明确，应该是黑白棋子的个数差的绝对值对于任意段均不超过 $k$。
    • 记忆化搜索，记 $f_{i,j,suf_i,suf_j}$ 为已经放了 $i$ 个白棋子，$j$ 个黑棋子，后缀分别有 $suf_i,suf_j$ 个棋子的方案数，搜到不合法或 $n+m$ 步返回即可。

66. 1106 模拟赛 - taxi (4/2)

    • 考试的时候没有看到只能坐 $4$ 个人。
    • 只需记下三个人的目的地，因为第四个人上车后必有人下车。所以记下当前乘客编号、当前司机位置以及车上三个人的目的地，分情况考虑转移，大力记搜即可。

67. 1106 模拟赛 - stone (2/1)

    • 折半枚举子集后将模意义下的和排序，枚举前一半，在后一半中 lower_bound 找即可。

68. P5322 [BJOI2019] 排兵布阵 (3/1)

    • 显然是背包，但不能对于每一组攻击都做一遍。
    • 考虑到如果攻占下一个玩家的城堡，那么出兵更弱的玩家自然也会被攻占，所以可以将 $a$ 数组排序，得到 $f_j = \max\{f_j, f_{j - a_{i,k}} \times 2 - 1\} + k \times i$。

69. P5337 [TJOI2019] 甲苯先生的字符串 (2/2)

    • 考虑构造一个 $26\times 26$ 的矩阵，原串里如果 $i,j$ 相邻则 $A_{i,j}=0$，否则 $A_{i,j}=1$。答案为 $A^{n-1}$。

70. P5319 [BJOI2019] 奥术神杖

    • Placeholder

71. CF464E The Classic Problem

    • Placeholder

72. P2900 [USACO08MAR] Land Acquisition G

    • Placeholder

73. P3195 [HNOI2008] 玩具装箱

    • Placeholder

74. CF240F TorCoder (3/3)

    • 对于每个区间修改，直接统计字符出现个数后判断奇偶，从 a 到 z 重构。对于字符集中的每个字符开一个线段树，代表这个区间内有多少个该字符。

75. CF383C Propagating tree (3/2)

    • 转化比较巧妙。直接将所有深度奇偶不同的点下传的正负不同（包括 update 和下传标记），这样保证了懒标记可以用线段树维护。

76. P4114 Qtree1 (1/3)

    • 树剖点权转边权模板，注意转化时的映射，以及题目中修改要求修改一条边的边权。

77. 1108 模拟赛 - 1 等差数列 (1/2)

    • 从左右边界暴力跳到第一个同时存在于两个等差数列中的数，再 $\Theta(1)$ 求即可。注意边界和细节。

78. 1108 模拟赛 - 2 玩具 (1/2)

    • 发现如果上半身无法走动时下半身占满了区间内所有的 $1$ 则无解。考虑用指针模拟整个运动过程，即将下半身移动到当前能到的最右端，再移动上半身到最右端，直到移动到整个区间的最右端。时间复杂度 $\Theta(n)$。

79. 1108 模拟赛 - 3 整除 (3/2)

    • 全场就我不会的水题。手写队列广搜，第一次搜到余数等于 $0$ 一定就是答案，输出事先记录下的前缀即可。

80. 1108 模拟赛 - 4 集合 (3/3)

    • 并查集按秩合并，即按照时间，将整个并查集结构重组成树形结构，每次向上找父亲的复杂度为 $\Theta(\log n)$。
    • 考虑每次询问时先找到该节点最晚的覆盖标记，再维护将最后一个覆盖标记之后的加法操作。由于是按秩合并，暴力向上跳的复杂度是正确的。

81. CF149D Coloring Brackets (2/3)

    • 区间 dp，显然设 $f_{l,r,i,j}$ 为对于 $[l,r]$ 这段区间左侧的括号颜色为 $i$，右侧为 $j$ 时的方案数。发现直接转移不太方便写，可以考虑使用记忆化搜索，每次只搜索合法的区间。

82. CF708C Centroids (4/2)

    • 树形 dp，可以先找出原树的重心，以重心为根，发现对于任意一个子节点作为根时若不满足重心的性质，一定是它父亲节点所在的子树大小超过了限制。由此可以将问题转化为求 $g_u$ 代表除子树 $u$ 外最大不超过 $\lfloor\frac{n}{2}\rfloor$ 的子树大小。最后统计答案是对于每一个点，如果它是重心或满足 $n-siz_u-g_u\le\lfloor\frac{n}{2}\rfloor$ 的条件则可以通过一次修改操作使它成为重心。
    • 考虑换根求 $g$，因为从 $u$ 转移到 $v$ 时可能 $v$ 已经是最大值，所以要记录最大值和次大值进行转移。

83. P5631 最小mex生成树 (4/2)

    • 有一个科技叫做可撤销并查集。即启发式合并后可以反悔操作的并查集。
    • 暴力的思路是从小到大枚举边权，判断删去这个边权后图是否联通，复杂度 $\Theta(mw\log m)$。考虑分治，分别考虑值域在 $[l,mid]$ 和 $[mid+1,r]$ 的边被删掉时图的连通性，分治后用可撤销并查集撤销操作。

84. P4099 [HEOI2013] SAO (5/3)

    • 题意是要求出一个树形图的不同的拓扑序个数。
    • 发现将原问题考虑成树形图将不好处理，所以直接在树上考虑树形 dp，对两种方向分别转移。设 $f_{u,i}$ 为在当前加进 $u$ 的子树中 $u$ 在子树的拓扑序排名为 $i$。
    • 将子树 $v$ 连到子树 $u$ 上，考虑两种情况：$u,v$ 之间的连边方向 $v$ 连向 $u$ 还是 $u$ 连向 $v$。贴张题解的分析：
    • 最后将与 $p$ 有关的项提出来，将 $f_{v,q}$ 前缀和优化一下，可以做到 $\Theta(n^2)$。

85. P2023 [AHOI2009] 维护序列 (1/2)

    • 复习了线段树同时维护乘法和加法时的优先级。

86. P2324 [SCOI2005] 骑士精神 (2/2)

    • IDA*（还是 A*，不太清楚），估价函数为有多少个棋子不在目标位置上。超过 $15$ 步则直接输出 -1。

87. P4133 [BJOI2012] 最多的方案

    • Placeholder

88. 1110 模拟赛 - 1 图 (2/1)

    • 非常直接的思路。考虑 bfs 过程中将 $s$ 到 $t$ 的最短路上每条边均染成不同的颜色，这样一定是最优的。bfs 过程中注意到 $t$ 了一定要直接 return，且尽可能少地留下不染色的边。

89. 1110 模拟赛 - 2 幂 (3/1, 80pts)

    • 100pts 的解法需要生成函数的知识，暂时咕着，NOIP 回来之后再补。
    • 80pts 可以将 $x$ 和括号分别考虑，发现就是一个组合数和卡特兰数的乘积求和，$\Theta(n^2)$ 预处理一下有 60pts，对于单点单独计算就可以达到 80pts 了。

90. 1110 模拟赛 - 3 异或 (4/2)

    • 排序不影响最后的结果，而且排完序后的序列有如下性质：$\forall 1\le a<b<c\le n,\min\{a \text{xor} b, b \text{xor} c\}\le a \text{xor} c$。证明可以按位分类讨论。根据上述性质容易想到 $\Theta(n^2)$ 的暴力 dp 转移。
    • 用 01-trie 优化这个过程。考虑在 01-trie 上查询每个元素对前边元素的贡献时，可以跳右子树（1）或跳左子树（0）的同时保留右子树的贡献，复杂度便优化到了 $\Theta(n\log x)$。

91. P4295 [SCOI2003] 严格N元树 (3/1)

    • 神奇的 dp 题。设 $f_i$ 为深度为 $i$ 的严格N元树的个数，则从上一层转移可以看作向上一层连接到了一个有 $n$ 个节点的根上，有转移方程 $f_i=f_{i-1}^n+1$。

92. P4035 [JSOI2008] 球形空间产生器 (3/1)

    • 高斯消元，需要一步转化：设球心坐标为 $(x_1,x_2,\cdots,x_n)$， 发现每个式子都可以写成形如 $\sum\limits_{j=0}^{n}(a_{i,j}-x_j)^2=c$ 的形式，其中 $c$ 是常数。将相邻的两个式子相减可以消去 $c$，整理后变成了可以高斯消元的形式。

93. P2607 [ZJOI2008] 骑士 (3/2)

    • 很妙的思路，值得借鉴。题目中给定了一个基环森林，对于每个连通块，考虑将环断开一条边，钦定这条边连接的两点必须只能选一个。然后再对删完边的树跑两遍形如“没有上司的舞会”的树形 dp 即可。

94. P3523 [POI2011] DYN-Dynamite (4/2)

    • 题目要求最大值最小，显然考虑二分答案。考虑树形 dp，从叶子向根处理，设 $f_u$ 为距 $u$ 最远的未被覆盖的关键点的距离，若没有则为 $-\infty$；设 $g_u$ 为 $u$ 到其子树下被选定节点的最小距离，若没有则为 $+\infty$。转移方程 $f_u=\max\{f_v+1\},g_u=\max\{g_v+1\}$。
    • 统计完子树贡献后分类考虑当前节点的贡献。若 $f_u+g_u\le mid$，则说明只用已选定节点中到 $x$ 距离最小的点就能够覆盖到最远的关键节点，此时整个子树已被覆盖，$f_u=-\infty$；若 $f_u=mid$，说明 $u$ 必须被选，此时将选点的个数加一；若 $g_u>mid$ 且 $d_u=1$ 则说明这个节点无法被其子节点覆盖，需要到父亲节点处解决，有 $f_u=\max\{f_u,0\}$。最后判断选择节点的个数和 $m$ 的关系进行二分答案即可。

95. P3174 [HAOI2009] 毛毛虫 (3/2)

    • 树形 dp，设 $f_u$ 为在 $u$ 的子树中，以 $u$ 为头的毛毛虫的最大毛毛虫的大小，显然有 $f_u=\max\limits_{v\in son_u}\{f_v\}+1+\max\{0,cnt_u-1\}$，其中 $cnt_u$ 指 $u$ 的儿子个数。
    • 发现最大的毛毛虫可能横跨两条这样的链，所以更新答案是同时维护最大值和次大值即可。

96. P4284 [SHOI2014] 概率充电器 (3/2)

    • 概率 + 树形 dp。根据套路，第一次计算子树内的贡献，第二次换根计算全局贡献。发现计算全局贡献时可能重复，所以区分更新前后的 dp 值，求出 $f_{last_u}$ 的转移式，再用其去转移 $f_{now_u}$。
    • 坑点：如果一个位置一定可以转移则直接转移，跳过转移方程的计算，因为这时转移方程中会出现分母为 $0$ 的情况。

97. P1131 [ZJOI2007] 时态同步 (3/2)

    • 贴一张绝妙的图解释本题的做法：
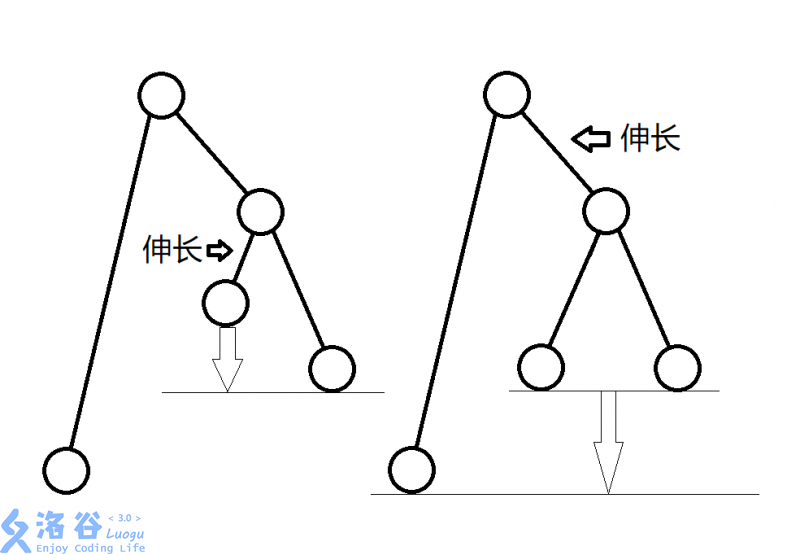
    • dfs 累加每次调整的代价。

98. P3812 【模板】线性基 (2/1)

    • 依次将原序列插入线性基，在线性基中从高位向低位枚举更新最大值。

99. CF468C Hack it! (4/0)

    • 发现 $\forall a < 10^{18}$，把 $[0,10^{18})$ 替换成 $[a,10^{18}+a)$，总代价会增加 $a$，所以有 $\sum\limits_{i=a-p}^{10^{18}+a-p-1}f_i\equiv 0 \mod a$，即 $l=a-p,r=10^{18}+a-p-1$ 时满足条件。

100. P5903 【模板】树上 k 级祖先 (1/2，倍增做法)

     • 可以长链剖分做到 $\Theta(n\log n)$ 预处理，$\Theta(1)$ 查询。倍增虽然每次查询是严格的 $\Theta(\log n)$，但表现优秀，可以通过本题。

101. P5431 【模板】乘法逆元 2 (2/1)

     • 发现原式可以通分一下，维护前缀后缀积，最后在乘上 $\prod a_i$ 的逆元即可。

102. P4822 [BJWC2012] 冻结 (1/2)

     • 分层图最短路模板，每层向下一层连一条边权为 $\dfrac{k}{2}$ 的边。

103. P2515 [HAOI2010] 软件安装 (3/2)

     • 将原图缩点后跑树形背包。
     • 坑点：图可能不联通，背包需要有超级源点。
     • 不要用 ~i 代替 i >= 0 的条件。

104. P4208 [JSOI2008] 最小生成树计数 (4/2)

     • 关键性质：在一个图的所有最小生成树中，每种边权出现的次数是固定的。

105. P4105 [HEOI2014]南园满地堆轻絮 (2/1)

     • Placeholder

106. P1772 [ZJOI2006] 物流运输 (3/3)

     • Placeholder

107. P2467 [SDOI2010] 地精部落 (4/1)

     • Placeholder

108. LOJ #2873. 「JOISC 2014 Day1」有趣的家庭菜园 (3/2)

     • Placeholder

109. P2319 [HNOI2006] 超级英雄 (2/2)

     • Placeholder

110. XJOI 1113 - A (2/2)

     • Placeholder

111. P3225 [HNOI2012] 矿场搭建 (3/3)

     • Placeholder

112. P5854 【模板】笛卡尔树 (2/1)

     • Placeholder

113. P5091 【模板】扩展欧拉定理 (3/1)

     • Placeholder

114. P7771 【模板】欧拉路径 (2/2)

     • Placeholder

115. 1115 模拟赛 - 1 mark (2/1)

     • 将原序列排序，双指针维护。二分最大差值，头指针右移的过程中如果与尾指针所指向的元素之差大于二分值则将尾指针右移。最后统计答案时加上二分位置右侧的一些值补全 $k$ 对。

116. 1115 模拟赛 - 2 gift (2/3)

     • 显然的状压 dp。先 bfs 求出所有礼物两两之间以及与起始、中止节点的距离，再状压，设 $f_{i,S}$ 为已经取了集合为 $S$ 的礼物，上一个取了 $i$ 的最短时间。

117. 1115 模拟赛 - 3 game (3/2)

     • 一个点能吃到其父亲节点的坚果当且仅当比它浅的节点都不选。树剖 + 线段树逐层维护。

118. 1115 模拟赛 - 4 medicine (3/2)

     • 树上背包套路化地利用 dfn 序映射成序列上的 01 背包 $\Theta(n^2)$ 处理。

119. P2279 [HNOI2003] 消防局的设立 (3/1)

     • 从叶子向上贪心考虑，如果当前节点距离最近的被覆盖点超过 $2$，则覆盖其祖父节点一定最优，因为其祖父节点还可以向上继续覆盖。

120. P1273 有线电视网 (4/2)

     • 树上分组背包，设 $f_{i,j}$ 为以 $i$ 为根节点的子树中选择 $j$ 个用户，能赚到的钱的最大值，将子树中选不同数量的用户视为不同的组，显然这些组互相冲突。
     • 转移方程 $f_{u,i}=\max\{f_{u,i-j}+f_{v,j}-e_w\}$，最后输出满足 $f_{1,i}\ge 0$ 最大的 $i$ 即为答案。

121. P1438 无聊的数列 (2/1)

     • 区间加等差数列，单点查询，等同于在差分序列中区间加区间求和。线段树或树状数组维护均可。

122. P2585 [ZJOI2006] 三色二叉树 (2/2)

     • 非常直接的思路，设 $f_{i,0/1/2}$ 为 $i$ 染成三种不同颜色时子树中最多有几个点被染成绿色，$g_{i,0/1/2}$ 为子树中最少有几个点被染成绿色，在序列上边加入新节点边转移即可。

123. CF1119A Ilya and a Colorful Walk (2/1)

     • 对于第一个数，从后向前找到最靠后的不与第一个数相同的位置，对最后一个数同理，取两个结果中较大的一个，一定是全局最优。

124. CF1119C Ramesses and Corner Inversion (2/1)

     • 每次变换时每行每列一定翻转偶数个格子，记录原矩阵和目标矩阵中不同的元素，如果每行每列不同元素的个数均为偶数则合法。

125. CF1119D Frets on Fire (2/2)

     • 原题目可以转化为数轴上的覆盖问题。将原序列排序后差分，再将差分数组排序，每次询问二分即可。

126. P7514 [省选联考 2021 A/B 卷] 卡牌游戏 (2/2)

     • 将 A、B 面放在一起排序，可以发现最终答案一定是中间一个连续段的左右端点之差。考虑用两个指针维护，保证一张牌的两面不被同时选择，同时保证选 A 面的张数不超过限制。

127. P2656 采蘑菇 (2/3)

     • 缩点 + dp。发现每个强连通分量内的边可以经过无数次，其他边只经过一次。将点权和边权同时考虑在缩点后的 DAG 上更新即可。

128. P1637 三元上升子序列 (2/1)

     • 树状数组维护 $a_i$ 之前有多少个数小于 $a_i$，以及 $a_i$ 之后有多少个数大于 $a_i$，对于每个位置计算两个值的乘积，将乘积求和即为答案。

129. P5094 [USACO04OPEN] MooFest (3/1)

     • 树状数组维护，发现最大值不方便处理，所以直接按照 $v$ 升序排序，分类讨论：
     • 设 $j < i$，对于 $x_i>x_j$ 的情况，可以用两个树状数组，一个统计有多少位置满足条件，另一个维护这些位置的和，答案即为 $x_i$ 乘以满足条件的 $j$ 的个数减去 $\sum x_j$。对于 $x_i<x_j$ 的情况直接用整体减去上述情况的值即可。

Records